Menentukan Rumus Fungsi Kuadrat Berdasarkan Grafik Yang Diketahui

 Menentukan Rumus Fungsi Kuadrat 

Berdasarkan Grafik Yang Diketahui

1. Diketahui Dua Titik Potong Grafik dengan Sumbu X

Titik potong dengan sumbu x terjadi ketika nilai y = 0. Sebuah grafik fungsi kuadrat paling banyak dapat memotong sumbu x sebanyak dua kali. Terdapat grafik fungsi kuadrat yang tidak memotong sumbu x. Ada juga grafik fungsi kuadrat yang hanya memotong sumbu x di satu titik.

Perhatikan gambar grafik fungsi kuadrat yang melalui dua buah titik pada sumbu x. Serta sebuah titik sembarang pada grafik berikut.

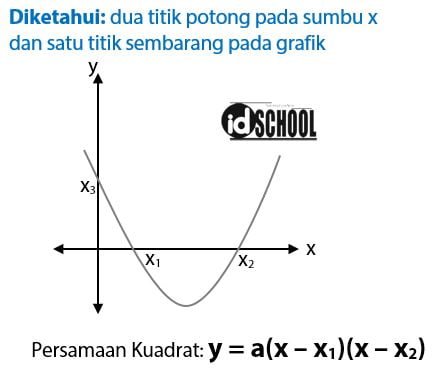
Cara mengetahui persamaan grafik fungsi kuadrat yang melalui sumbu x pada dua titik bisa dilakukan cara ini. Misalkan diketahui sebuah grafik fungsi kuadrat yang memotong sumbu x di titik (x1, 0) dan (x2, 0). Persamaan yang mewakili persamaan kuadrat tersebut adalah y = (x – x1)(x – x2) = 0.

Bentuk umum persamaan kuadrat di atas berlaku saat grafik memotong sumbu x di A( x1, 0 ), B( x2, 0 ) dan C (x3, y3). Untuk menambah pemahaman sobat idschool, perhatikan contoh soal dan pembahasannya berikut.

Contoh 1: Menentukan Persamaan Kuadrat Jika Diketahui Gambar

Perhatikan gambar di bawah!

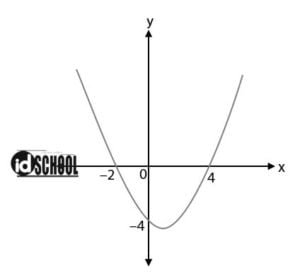
Persamaan grafik fungsi kuadrat pada gambar di atas adalah ….
A.   y = x² – ½x – 8
B.   y = x² – ½x – 4
C.   y = ½x² – x – 4
D.   y = ½x² – x – 8
E.   y = ½x² – 2x – 8

Pembahasan:

Diketahui dua titik yang memotong sumbu x adalah  (–2, 0) dan (4, 0). Diketahui juga sebuah titik pada grafik fungsi kuadrat (0, –4).

Mencari nilai A:
y = a (x – x1)(x – x2)
–4 = a(0 – (–2))(0 – 4)
–4 = a × 2 × (–4)
–4 = a(–8)
a = –4/–8
a = ½

Mencari persamaan kuadrat:
y = a(x – x1)(x – x2)
y = ½ (x + 2)(x – 4)
y = ½ (x² – 2x – 8)
y = ½x² – x – 4

Jadi, persamaan grafik fungsi kuadrat pada gambar di atas adalah y = ½x² – x – 4.

Jawaban: C

Baca Juga 5 Langkah Menggambar Grafik Fungsi Kuadrat

#2: Diketahui Titik Puncak dan Titik Potong dengan sumbu – y

Berikutnya adalah kondisi soal untuk gambar grafik fungsi kuadrat dengan titik puncak dan satu titik memotong sumbu y. Bentuk umum persamaan kuadrat yang digunakan untuk menyelesaikan jenis soal ini adalah y = a(x – xp) + yp. Perhatikan gambar grafik fungsi kuadrat dengan diketahui titik puncak (xp, yp) dan satu titik pada grafik fungsi kuadrat berikut.

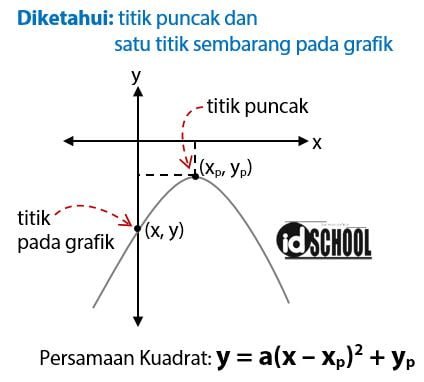
Simak contoh soal dan pembahasan yang sesuai dengan kondisi tersebut pada soal berikut.

Contoh 2: Cara Menentukan Persamaan Kuadrat Jika Diketahui Gambar

Perhatikan gambar di bawah!

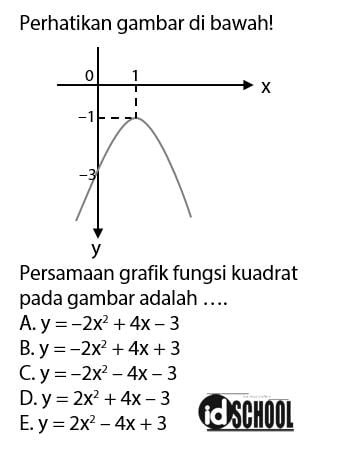
Pembahasan:

Diketahui dari gambar grafik fungsi pada soal:

• koordinat titik puncak (1, –1)
• grafik melalui titik (0, –3)

Mencari nilai a:
y = a(x – xp)2 + yp
–3 = a(0 – 1)2 + (–1)
–3 = a × 1 – 1
–3 = a – 1
a = –3 + 1 = –2

Mencari persamaan kuadrat:
y = –2(x – 1)2 + (–1)
y = –2(x2 – 2x + 1) –1
y = –2x2 + 4x – 3

Jawaban: A

Baca Juga: Pertidaksamaan Kuadrat dan Himpunan Penyelesaiannya

#3: Diketahui Tiga Titik Sembarang pada Grafik Fungsi Kuadrat

Cara yang ketiga adalah untuk mengetahui persamaan grafik fungsi kuadrat dengan diketahui tiga titik koordinat. Tiga titik koordinat tersebut terletak pada grafik fungsi kuadrat. Kondisi soal seperti ini bisa diselesaikan dengan menggunakan bentuk umum persamaan kuadrat y = ax2 + bx + c.

Substitusikan ketiga titik koordinat pada grafik fungsi kuadrat sehingga diperoleh tiga persamaan linear. Tiga buah persamaan linear tersebut terdiri dari tiga buah variabel a, b, dan c. Selanjutnya, gunakan metode elimiasi dan substitusi untuk mendapatkan nilia a, b, dan c. Pada akhirnya akan diperoleh persamaan kuadrat yang sesuai.

Untuk menambah pemahaman sobat idschool, simak contoh soal berikut.

Contoh 3: Soal Menentukan Persamaan Kuadrat Jika Diketahui Gambar

Perhatikan gambar berikut!

Persamaan dari grafik fungsi di atas adalah ….
A. f(x) = 4/5 x2 – x – 4/5
B. f(x) = 3x2 – 4/5x – 4/5
C. f(x) = 4/5x2 – 3x + 4/5
D. f(x) = 4/5x2 + 3x – 4/5
E. f(x) = 4/5x2 – 3x – 4/5

Pembahasan:

Grafik fungsi di atas melalui tiga buah titik yaitu (–1, 3), (1, –3), dan (4, 0). Bentuk umum persamaan kuadrat yang digunakan adalah: y = ax2 + bx + c.

Substitusi tiga titik pada bentuk umum persamaan kuadrat:

• Persamaan (1): untuk titik (–1, 3)
  f(x) = ax2 + bx + c
  3 = a(–1)2 + b(–1) + c
  3 = a – b + c → a – b + c = 3
  
• Persamaan 2: untuk titik (1, –3)
  f(x) = ax2 + bx + c
  –3 = a(1)2 + b(1) + c
  –3 = a + b + c → a + b + c = –3
  
• Persamaan 3: untuk titik (4, 0)
  f(x) = ax2+bx+c
  0 = a(4)2 + b(4) + c
  0 = 16a–4b+c → 16a–4b + c = 0

Berikutnya adalah mencari nilai a, b, dan c dengan metode eliminasi dan subsitusi. Eliminasi a dan b dari persamaan (1) dan (2) untuk mendapatkan nilai b:

Diperoleh nilai b = –3, selanjutnya adalah mencari nilai a dan c. Eliminasi c dari persamaan (1) dan (3):

Subtitusi nilai b = –3 pada persamaan 15a + 5b = – 3 untuk mendapatkan nilai a.

15a + 5(–3) = –3
15a = –3+15
15a = 12
a = 12/15 = 4/5

Substitusikan nilai a = 4/5 dan b = – 3 ke persamaan (1) untuk mendapatkan nilai c:
a – b + c = 3
4/5 – (–3) + c = 3
4/5 + 3 + c = 3
c = 3 – 3 – 4/5
c = – 4/5

Langkah terakhir, substitusi nilai a, b, dan c yang diperoleh pada bentuk umum persamaan grafik fungsi kuadrat f(x) = ax2 + bx + c. Jadi persamaan grafik fungsi kuadrat di atas adalah f(x) = 4/5x2 + (–3)x + (–4/5) = 4/5x2 – 3x – 4/5.

Jawaban: E